머신러닝(검증)

Cross Validation

1. Train, Valid, Test Set

훈련, 검증, 테스트 데이터라고 부르는 3가지를 한번 이야기 해보겠습니다.

• Train Data : 모델을 학습하는데 사용하는 데이터 (모델이 알고 있는 학습할 데이터)
• Valid Data : 학습한 모델의 성능을 검증하는 데이터 (모델이 모르는 학습하지 않을 데이터, 모델 검증에 사용하는 데이터)
• Test Data : 학습한 모델로 예측할 데이터 (모델이 모르는 예측할 데이터)

2. k-fold with stratify

k-fold는 데이터를 k개로 쪼개는 것을 말합니다.
일반적으로 Cross Validation에서 사용되며, 데이터셋을 k개로 쪼개어 k-1개로 모델을 학습하고, 1개로 모델을 검증합니다.
k개로 데이터를 쪼개면, 모든 fold에 대해(하나의 fold를 선택하여) 검증하는 방식으로 k번 다른 데이터셋으로 학습한 모델을 검증할 수 있습니다.

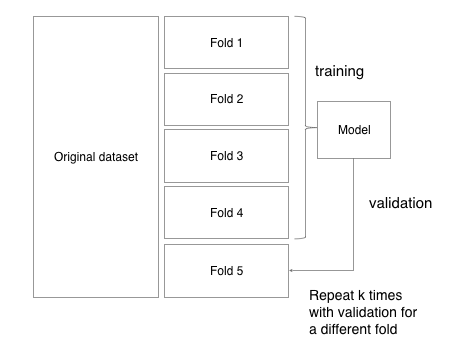
Stratify, 계층적 k-fold

k-fold는 데이터의 정렬 유무와 분류할 클래스의 비율에 상관없이 순서대로 데이터를 분할하는 특징이 있습니다.
하지만, 분류할 클래스의 비율이 다르다면 어떻게 될까요? 그런 경우에는, 각 fold가 학습 데이터셋을 대표한다고 말하기 어려워집니다.
한 fold에 특정 클래스가 많이 나올수도, 적게 나올수도 있기 때문입니다. Stratified k-fold는 그러한 문제점을 해결하기 위해 제안되었습니다.
k개의 fold도 분할한 이후에도, 전체 훈련 데이터의 클래스 비율과 각 fold가 가지고 있는 클래스의 비율을 맞추어 준다는 점이 기존의 k-fold와의 다른 특징 입니다.

k-fold는 sklearn의 model_selection 패키지에 있습니다.

Cross Validation

1. 데이터 집합을 k개의 데이터 Fold로 나눕니다. (k-1)개의 Fold는 훈련 Fold, 1개는 검증 Fold로 지정합니다.
2. 훈련 Fold를 이용하여 모델을 훈련시키고, 검증 Fold를 이용하여 정확도를 측정합니다. 동시에 훈련 과정에서 구한 parameter 값들을 저장합니다.
3. 1-2번 과정을 k번 반복합니다. 이 때, 한 번 선정한 검증 Fold를 중복하여 선택하지 않습니다.
4. 전체 시험 정확도의 평균을 k에 대한 모델의 정확도로 이용합니다. 이 때, 저장한 parameter 값들에 대한 평균을 내어 최종적인 매개 변수로 이용합니다.

  print('cross validation : {:.2f}% '.format(np.mean(cross_val_score(rf,kf_data,kf_label,cv=5))*100))

-> rf는 모델 cv는 나누는 횟수

Parameter Tuning

GridSearch

모델 하이퍼 파라미터에 넣을 수 있는 값들을 순차적으로 입력한뒤에 가장 높은 성능을 보이는 하이퍼 파라미터들을 찾는 탐색 방법이다.

GridSearchCV 함수는 Sklearn의 model_selection 패키지에 있다.

파라미터란 학습 과정에서 생성되는 변수이다.

하이퍼 파라미터란 모델을 생성할 때, 사용자가 직접 설정하는 변수이다.

    from sklearn.linear_model import LogisticRegression
    from sklearn.model_selection import GridSearchCV
    rf = RandomForestClassifier()

    LR = LogisticRegression(penalty='l2')
    GV = GridSearchCV(LR, param_grid={'c':[0.001, 0.01, 0.1]},scoring='accuracy', cv=4)

    GV = GV.fit(x_train,y_train)
    y_train = GV.predict(x_test)

### Random search

모든 경우를 격자로 탐색하는 그리드 서치와 다르게 랜덤 서치는 하이퍼 파리미터 값을 랜덤하게 넣어보고 그중 가장 우수한 값을 보인 하이퍼 파라미터를 활용해 모델을 생성한다.

• 장점 : 불필요한 탐색 횟수를 줄인다.

Bayesian Optimization

Grid는 시간이 오래걸린다는 단점이 있고 Random은 정확도가 다소 떨어진다. Bayesian Optimization은 효율적으로 최적값을 찾아낸다는 장점이 있다.

핵심은 사전 정보를 최적값 탐색에 반영하는 것인데 기존 입력값들을 바탕으로 미지의 목적 함수 f의 형태에 대한 확률적인 추정을 하는 방식이다.

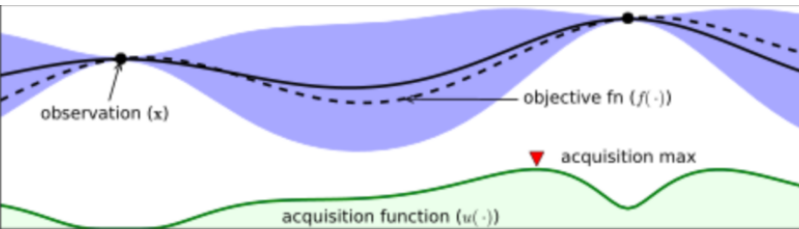
• 검은색 실선은 우리가 찾으려고 하는 목점함수이다.
• 검정색 점선은 지금까지 관측한 데이터를 바탕으로 우리가 예측한 Estimated function을 의미한다.
• 파란 영역은 목점함수(f(x))가 존재할만한 영역이다.
• Acquisition function 값이 컸던 지점의 function 값을 관측하고 estimation을 update한다.

XGBoost of 하이퍼 파라미터 여기 링크에 XGBoost에서 사용하는 하이퍼 파라미터와 코드가 나와있다.