머신러닝(분류)

Classification

머신러닝과 통계학에서의 분류는 새로 관측된 데이터가 어떤 범주 집합에 속하는지를 식별하는 것을 말합니다.
훈련 데이터를 이용해 모델을 학습하면, 모델은 결정 경계(Decision boundary)라는 데이터를 분류하는 선을 만들어 냅니다.

1. Logistic Regression

로지스틱 회귀는 회귀를 사용하여 데이터가 어떤 범주에 속할 확률을 0에서 1 사이의 값으로 예측하고 그 확률에 따라 가능성이 더 높은 범주에 속하는 것으로 분류해주는 지도 학습 알고리즘이다.

예를들어, 스팸 메일 같은 경우 어떤 메일을 받았을 때 스팸일 확률이 0.5 이상이면 스팸메일로 분류하고, 0.5보다 작은 경우 일반메일로 분류하는 것이다.(2진분류)

    from sklearn.linear_model import LogisticRegression
    lr = LogisticRegression()
    lr.fit(x_train, y_train)
    y_pred = lr.predict(x_test)     

• 결과 살펴보기

일반적으로 분류에서는 Accuaracy, 정확도를 평가 척도로 사용합니다.

    from sklearn.metrics import accuracy_score
    print('로지스틱 회귀, 정확도 : {:.2f}%'.format(accuracy_score(y_test, y_pred)*100))

2. Support Vector Machine

Support Vector Machine(SVM, 서포트 벡터 머신)는 주어진 데이터를 바탕으로하여 두 카테고리(이진 분류의 경우) 사이의 간격(Margin, 마진)을 최대화하는 데이터 포인트(Support Vector, 서포트 벡터)를 찾아내고,
그 서포트 벡터에 수직인 경계를 통해 데이터를 분류하는 알고리즘입니다.

Cost : Soft or Hard

SVM에는 Soft Margin, Hard Margin 이라는 말이 있습니다. 단어 자체에서도 유추할 수 있으시겠지만, Soft Margin은 유연한 경계면을 만들어내고 Hard Margin은 분명하게 나누는 경계면을 만들어냅니다. 그렇다면 왜 Soft Margin이 필요한걸까요?

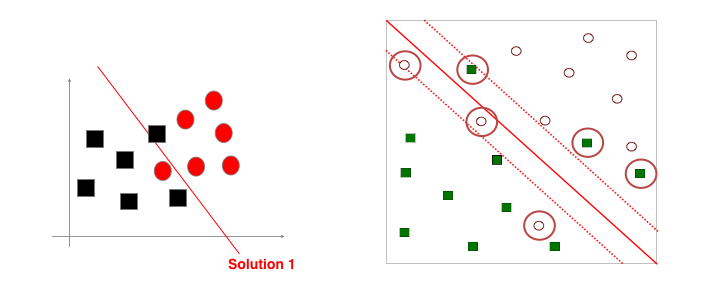
다음과 같은 데이터 분포는 직선으로 두개의 데이터를 나누는 경계면을 만들기 어렵습니다. 현실에서도 우리가 최적의 답을 찾지 못할때 어느정도 비용(Cost, C)을 감수하면서 적절한 답을 찾는 것을 떠올려보세요.
Soft Margin은 그런 원리입니다. 경계면을 조금씩 넘어가는 데이터들(비용, Cost)을 감수하면서 가장 차선의 경계면을 찾습니다.
실제 알고리즘에서도 C(Cost)값을 통해 얼마나 비용을 감수할 것인지를 결정할 수 있습니다. 크면 클수록 Hard Margin을, 작으면 작을수록 Soft Margin을 만들어냅니다.

저차원을 고차원으로 Kernel Trick

SVM은 기본적으로 선형 분류를 위한 경계면을 만들어냅니다. 그렇다면 어떻게 비선형 분류를 할 수 있을까요?

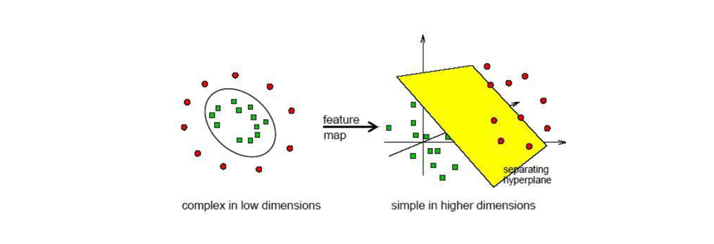
저차원(2차원)에서는 선형 분리가 되지 않을 수 있지만, 고차원(3차원)에서는 선형 분리가 가능할 수 있습니다.
이러한 원리를 바탕으로 선형 분리가 불가능한 저차원 데이터를 선형 분리가 가능한 어떤 고차원으로 보내 선형 분리를 할 수 있습니다.
하지만, 저차원 데이터를 고차원으로 보내서 서포트 벡터를 구하고 저차원으로 내리는 과정에서 더 복잡해지고 연산량도 많아질것이 분명합니다.
그래서 여기에서 Kernel Trick이라는 Mapping 함수를 사용합니다. Kernel Trick은 고차원 Mapping과 고차원에서의 내적 연산을 한번에 할 수 있는 방법입니다.
이를 통해 여러가지 Kernel 함수를 통해 저차원에서 해결하지 못한 선형 분리를 고차원에서 해결할 수 있습니다.

대표적인 Kernel 함수

• Linear (선형 함수)
• Poly (다항식 함수)
• RBF (방사기저 함수)
• Hyper-Tangent (쌍곡선 탄젠트 함수)

서포트 벡터 머신 분류기는 Sklearn의 svm 패키지에 있습니다.

    #모델 불러오기 및 정의하기
    from sklearn.svm import SVC
    svc = SVC()
    # 모델 학습하기(훈련 데이터)
    svc.fit(x_train, y_train)
    # 결과 예측하기(테스트 데이터)
    y_pred = svc.predict(x_test)
    # 결과 살펴보기
    print('서포트 벡터 머신, 정확도 : {:.2f}%'.format(accuracy_score(y_test, y_pred)*100))

Decision Tree

결정 트리는 입력 변수를 특정한 기준으로 잘라(분기) 트리 형태의 구조로 분류를 하는 모델입니다.

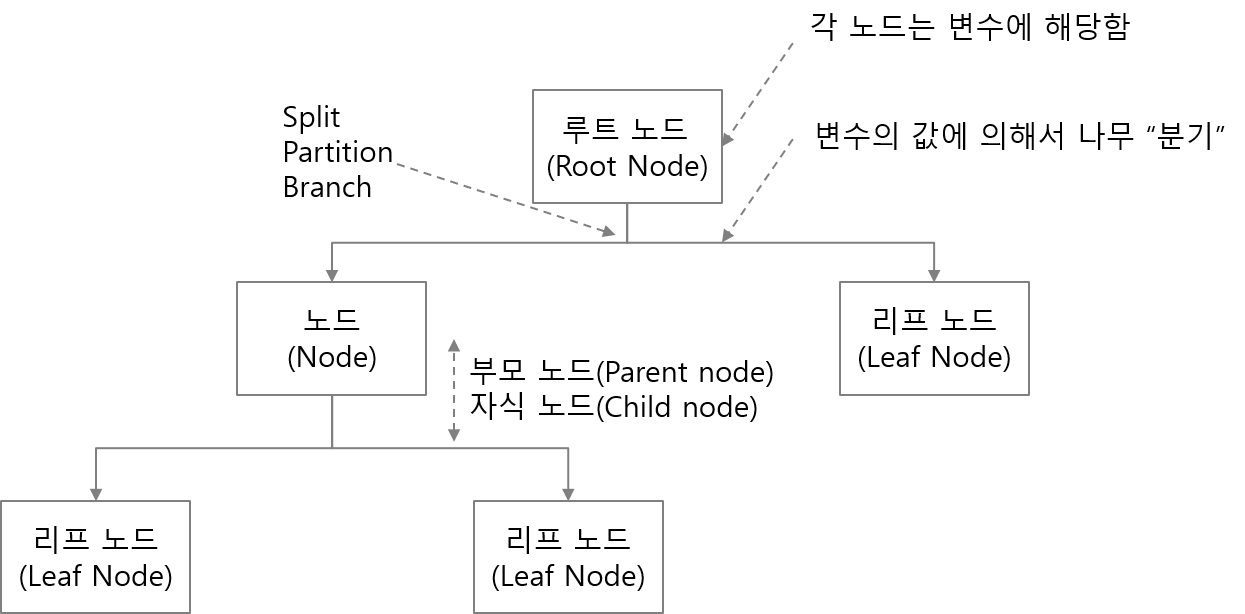
• 사람의 논리적 사고 방식을 모사하는 분류 방법론
• IF-THEN rule의 조합으로 class 분류
• 결과를 나무 모양으로 그릴 수 있음
• Greedy 한 알고리즘 (한번 분기하면 이후에 최적의 트리 형태가 발견되더라도 되돌리지 않음, 최적의 트리 생성을 보장하지 않음)
• 축에 직교하는 분기점
• 데이터 전처리가 필요 없음

불순도(Impurity, Entropy)

결정 트리는 데이터의 불순도를 최소화 할 수 있는 방향으로 트리를 분기합니다.
불순도란 정보 이론(Information Theory)에서 말하는 얻을 수 있는 정보량이 많은 정도를 뜻합니다.
ex) 오늘 해가 동쪽에서 뜰꺼야 -> 낮은 정보량, 오늘 일식이 일어날꺼야 -> 높은 정보량

결정 트리 모델은 Sklearn의 tree 패키지에 있습니다.

    from sklearn.tree import DecisionTreeClassifier
    dt = DecisionTreeClassifier(max_depth=5)

Random Forest

결정 트리가 나무였다면, 랜덤 포레스트는 숲 입니다. 랜덤 포레스트의 특징은 작은 트리들을 여러개 만들어 합치는 모델입니다.
서로 다른 변수 셋으로 여러 트리를 생성합니다. 여러개의 모델을 합치는 앙상블 기법 중 대표적인 예시입니다.

    from sklearn.ensemble import RandomForestClassifier
    rf = RandomForestClassifier(max_depth=5,)

K Nearest Neighbors

1. K-Means 클러스터링과 유사하게 유클리드거리를 이용하여 점과 점사이의 거리를 계산합니다.

2. 최근접 이웃 사이에서 가장 공통적인 항목에 할당되는 객체로 과반수 의결에 의해 분류된다.

3. 단순히 데이터를 저장하기 때문에 모델 생성이 빠릅니다.

4. 거리 계산이 많기 때문에 예측 속도가 느리고 데이터 세터가 큰 경우 많은 메모리를 요구합니다.

    from sklearn.neighbors import KneighborsClassifier
    #이웃한 3개의 점 중에서 과반수로 결정한다.
    KNN = KneighborsClassifier(n_neighbors=3)
    KNN = KNN.fit(x_data,y_data)
    y_predict=KNN.predict(x_data)

Naïve Bayes

• 데이터가 각 클래스에 속할 특징 확률을 계산하는 조건부 확률 기반의 분류 방법이다.

• 사건 B가 주어졌을 때 사건 A가 일어날 확률인 P(A

  B), 조건부 확률과 베이즈 정리를 이용한 분류이다.

• 분류별 값이 나오고 그 값들을 더 해 그 중 가장 높은 확률을 선택한다.
• 스팸 필터링, 의학적 질병 진단, 문서 분류 등에 자주 사용한다.

    from sklearn.naive_bayes import BernoulliNB
    BNB = BernoulliNB(alpha=1.0)
    BNB = BNB.fit(x_train,y_train)
    y_predict = BNB.predict(x_test)

Evaluation

1. Accuracy, 정확도

모든 데이터에 대해 클래스 라벨을 얼마나 잘 맞췄는지를 계산

• Precision, 정밀도 : TP/(FP+TP), 1이라고 예측한 것 중 실제로 1인 것
• Sensitivity, 민감도 : True Positive rate = Recall = Hit ratio = TP/(TP+FN), 실제로 1인 것 중에 1이라고 예측한 것
• Specificity, 특이도 : True Negative rate = TN/(FP+TN), 실제로 0인 것 중에 0이라고 예측한 것
• False Alarm, 오탐 : False Positive rate = 1-Specificity = FP/(FP+TN), 실제로 0인 것 중에 1이라고 예측한 것

    print('Accuracy : {:.3f}'.format(accuracy_score(y_test, y_pred)))
    print('Precision : {:.3f}'.format(precision_score(y_test, y_pred)))
    print('Recall : {:.3f}'.format(recall_score(y_test, y_pred)))
    print('AUC : {:.3f}'.format(roc_auc_score(y_test, y_pred)))