머신러닝(회귀)

단순회귀 분석

일반적으로 소득이 증가하면 소비도 증가하는 것처럼, 어떤 변수(독립 변수 X)가 다른 변수(종속 변수 Y)에 영향을 준다면 두 변수 사이에 선형 관계가 있다고 이야기한다. 이와 같은 선형관계를 알고 있다면 새로운 독립 변수 X 값이 주어졌을 때 거기에 대응되는 종속 변수 Y 값을 예측 할 수 있다. 이처럼 두 변수 사이에 일대일로 대응되는 확률적, 통계적 상관성을 찾는 알고리즘을 단순회귀 분석이라고 한다.

선형 회귀분석의 4가지 기본 가정

선형 회귀에는 4가지 가정이 필요하다.

1. 선형성
2. 독립성
3. 등분산성
4. 정규성

1. Simple Linear Regression

x가 1개인 단순회귀 분석

x 변수로 ‘RM’ 변수를, y 변수는 주택 가격으로 하겠습니다.
Linear Regression은 Sklearn의 linear_model 패키지에 있습니다.

• 회귀부터는 데이터를 train, test로 나누어 진행한다. sklearn의 model_selection 패키지에 있는 train_test_split 함수를 사용합니다.

          
        from sklearn.model_selection import train_test_split
        x_train, x_test, y_train, y_test = train_test_split(data, label, test_size=0.2, random_state=2019)
        #모델 불러오기 및 정의하기
        from sklearn.linear_model import LinearRegression
        sim_lr = LinearRegression()
        #모델 학습하기(훈련 데이터)
        sim_lr.fit(x_train['RM'].values.reshape((-1, 1)), y_train)
        #결과 예측하기
        y_pred = sim_lr.predict(x_test['RM'].values.reshape((-1, 1)))
        y_pred
        #결과 살펴보기
        from sklearn.metrics import r2_score
        print('단순 선형 회귀, R2 : {:.4f}'.format(r2_score(y_test, y_pred)))
        line_x = np.linspace(np.min(x_test['RM']), np.max(x_test['RM']), 10)
        line_y = sim_lr.predict(line_x.reshape((-1, 1)))
  
        plt.scatter(x_test['RM'], y_test, s=10, c='black')
        plt.plot(line_x, line_y, c = 'red')
        plt.legend(['Regression line', 'Test data sample'], loc='upper left')
  

  다중선형회귀는 x_train 값을 그대로 넣는 것이다.

Machine Learning Algorithm Based Regression

머신러닝 알고리즘을 기반으로한 회귀 모델입니다. Sklearn이 지원하는 머신러닝 기반 회귀 모델로는 결정 트리, 랜덤 포레스트, 서포트 벡터 머신, MLP, AdaBoost, Gradient Boosting 등이 있다.

1. Decision Tree Regressor

트리 모델은 데이터의 불순도(impurity, Entropy)를 최소화 하는 방향으로 트리를 분기하여 모델을 생성합니다. 결정 트리 회귀 모델은 Sklearn의 tree 패키지에 있습니다.

    from sklearn.tree import DecisionTreeRegressor
    dt_regre = DecisionTreeRegressor(max_depth=5)
    dt_regre.fit(x_train, y_train)
    y_pred = dt_regre.predict(x_test)
    print('다중 결정 트리 회귀, R2 : {:.4f}'.format(r2_score(y_test, y_pred)))

2. Support Vector Machine Regressor

서포트 벡터 머신의 기본 개념은 결정 경계와 가장 가까운 데이터 샘플의 거리(Margin)을 최대화 하는 방식으로 모델을 조정합니다.
서포트 벡터 머신 회귀 모델은 Sklearn의 svm 패키지에 있습니다.

    from sklearn.svm import SVR
    svm_regr = SVR(C=20,kernel='poly')
    svm_regr.fit(x_train, y_train)
    y_pred = svm_regr.predict(x_test)
    print('다중 서포트 벡터 머신 회귀, R2 : {:.4f}'.format(r2_score(y_test, y_pred)))

3. Multi Layer Perceptron Regressor

딥러닝의 기본 모델인 뉴럴 네트워크를 기반으로 한 회귀 모델입니다. 기본적으로 MLP라 하면, 입력층-은닉층-출력층 3개로 이루어진 뉴럴 네트워크를 의미합니다.

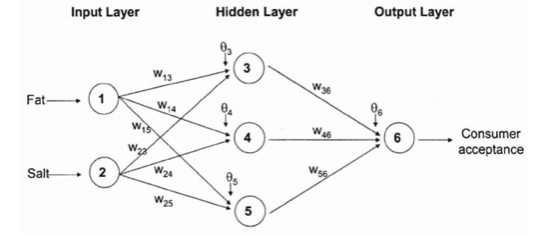
어떻게 뉴럴 네트워크가 비선형 문제를 해결할 수 있을까?

은닉층에 존재하는 하나하나의 노드는 기본 선형 회귀 모델과 동일하게 wx + b 로 이루어져 있습니다.
하지만 이런 선형 분리를 할 수 있는 모델을 여러개를 모아 비선형 분리를 수행하는 것이 뉴럴 네트워크 입니다.

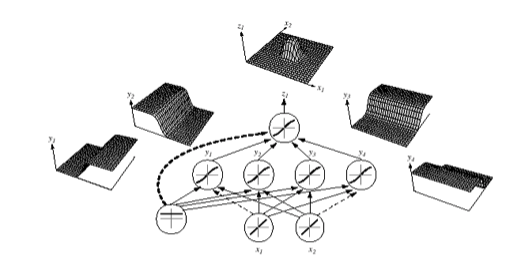
아래 그림을 보면 4개의 벡터 공간을 선형 분리하는 퍼셉트론들이 하나의 비선형 공간을 분류할 수 있는 벡터 공간을 형성하는 것을 확인할 수 있습니다.
직관적으로는 이해하기 어려우시겠지만, 우리가 케익을 4개의 퍼셉트론들이 분할하는 대로 잘라 가운데 부분을 남기는 것을 생각해보시면 되겠습니다.

MLP 회귀 모델은 Sklearn의 neural_network 패키지에 있습니다.

    from sklearn.neural_network import MLPRegressor
    mlp_regr = MLPRegressor(hidden_layer_sizes=(50, ), activation='tanh', solver ='sgd', random_state=2019)
    mlp_regr.fit(x_train, y_train)
     y_pred = mlp_regr.predict(x_test)
    print('다중 MLP 회귀, R2 : {:.4f}'.forma(r2_score(y_test, y_pred)))

Ridge Regression(L2 Norm)

Ridge regression은 최소제곱법과 매우 유사하나, ‘각 계수의 제곱을 더한 값’을 식에 포함하여 계수의 크기도 함께 최소화하도록 만들었다

    from sklearn.linear_model import Ridge
    l2 = Ridge(alpha=0.05,normalize=True)

Lasso Regression(L1 Norm)

Lasso는 최소제곱법과 유사하나, ‘각 계수 절댓값의 합’을 수식에 포함하여 계수의 크기도 함께 최소화하도록 만들었다.

    from sklearn.linear_model import Lasso
    l1 = Lasso(alpha=0.05,normalize=True)
    l1.fit(x_train,y_train)